Introduction to Different types of Line:
A line is the collection of points, along a straight line path and going to opposite direction, and also a line segment is part of a line, it’s having two end points. A ray also a part of line, one side is endpoint and other side goes to one direction.
A line doesn’t have starting point imagine it is endless from both directions. A continuous level of the length contains more than two points. Put the little arrows on both sides for understanding.
Different Types of lines:
In the following three different types of lines:
Parallel line,
Perpendicular line, and
Intersecting line.
These three are the most important types of line in math.
Explain the different types of line:
1. Parallel line
It is one of the important line in math, It having two lines, both in the same plane, Lines are remain the same distance but never touching each other going to same direction.
Example :-
1. Solve:-
r is parallel to s
angle 1 = 60 degrees
To find the measures of seven angles in an accompanying figure (below).
Solution:
An Angle 2 = 120 degrees is supplementary to angle 1.These angles are any two angles whose sum is 180 degrees.
An Angle 3 = 60 degrees since angle 1 and Angle 3 are vertical angles. The two nonadjacent angles are formed by two intersecting lines.
An Angle 4 = 120 degrees is supplementary to angle 1.
An Angle 5 = angle 1 by the transversal Postulate.
An Angle 6 = angle 2, Angle 7 = angle 3, and Angle 8 = angle 4 by the transversal Postulate
2. Perpendicular line
It is the another type of line in math, it is having 2 lines (Perpendicular) that lines intersect and form right angles are called perpendicular lines and other lines otherwise intersect the right angles.
Ex:1 Determine if y = 2x+5 and x+2y = -2 are perpendicular then graph the equations to check.
Equation
1) y = 2x+5
2) x+2y = -2
Slope Intercept Form
y = 2x+5
y = (-1/2)x-2
Slope
2(-1/2)
The slope of the line is [2*(-1/2)]= -1, the two lines are perpendicular.
3. Intersecting lines
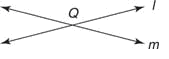
This is the last one of the types of lines in math, Two different lines or more than two different lines that meet at a point is called as intersecting lines.Here in diagram line l and line m intersect at point Q
A line contains both ends having an end points that is known as line segments.
Ex:1. The Intersecting lines are lines that meet at a point. When two intersect lines, they define angles point of intersection.

at point C.
A line is the collection of points, along a straight line path and going to opposite direction, and also a line segment is part of a line, it’s having two end points. A ray also a part of line, one side is endpoint and other side goes to one direction.
A line doesn’t have starting point imagine it is endless from both directions. A continuous level of the length contains more than two points. Put the little arrows on both sides for understanding.
Different Types of lines:
In the following three different types of lines:
Parallel line,
Perpendicular line, and
Intersecting line.
These three are the most important types of line in math.
Explain the different types of line:
1. Parallel line
It is one of the important line in math, It having two lines, both in the same plane, Lines are remain the same distance but never touching each other going to same direction.
Example :-
1. Solve:-
r is parallel to s
angle 1 = 60 degrees
To find the measures of seven angles in an accompanying figure (below).
Solution:
An Angle 2 = 120 degrees is supplementary to angle 1.These angles are any two angles whose sum is 180 degrees.
An Angle 3 = 60 degrees since angle 1 and Angle 3 are vertical angles. The two nonadjacent angles are formed by two intersecting lines.
An Angle 4 = 120 degrees is supplementary to angle 1.
An Angle 5 = angle 1 by the transversal Postulate.
An Angle 6 = angle 2, Angle 7 = angle 3, and Angle 8 = angle 4 by the transversal Postulate
2. Perpendicular line
It is the another type of line in math, it is having 2 lines (Perpendicular) that lines intersect and form right angles are called perpendicular lines and other lines otherwise intersect the right angles.
Ex:1 Determine if y = 2x+5 and x+2y = -2 are perpendicular then graph the equations to check.
Equation
1) y = 2x+5
2) x+2y = -2
Slope Intercept Form
y = 2x+5
y = (-1/2)x-2
Slope
2(-1/2)
The slope of the line is [2*(-1/2)]= -1, the two lines are perpendicular.
3. Intersecting lines
This is the last one of the types of lines in math, Two different lines or more than two different lines that meet at a point is called as intersecting lines.Here in diagram line l and line m intersect at point Q
A line contains both ends having an end points that is known as line segments.
Ex:1. The Intersecting lines are lines that meet at a point. When two intersect lines, they define angles point of intersection.

at point C.